Introduction

Efforts to describe atoms have always straddled the worlds of philosophy and science. Despite hardened disciplinary boundaries, we see atoms whiz nonchalantly across widely different academic departments, often turning up in linguistics, logic, history or sociology. However, if we consider for a moment that humans have been wondering, “But what is this or that made of, really?!” for a very long time, such blurred boundaries seem inevitable. Atoms are, quite literally, too fundamental to have truck only with chemists and physicists of varying persuasions.

But what is this made of, really?

The search for a primordial substance goes back thousands of years. The ancient Indian concept of pañcabhūta (literally, five elements, namely, air, water, fire, earth and ether) and the similarly ancient Chinese concept of wǔxíng (again, five elements, represented by wood, fire, earth, metal and water) illustrate approaches that sought to express all creation and their interactions in terms of fundamental components. Shadows of these ideas have been traced back to texts dating as far back as the 9^th century BCE.¹ Around 600 BCE, the famed Greek philosopher, Thales of Miletus, speculated on the existence of such substances and identified water as the primordial substance from which everything else arose. In his wake, Anaximander upheld the idea of one primordial substance, but placed the essence of matter ‘beyond the level of an observable material substance’, while Empedocles expanded the set of primordial substances to four. ² It pays to note that similar ideas are still a part of indigenous knowledge traditions across the world, and their interconnectedness and independence are still a matter of much debate. For example, many indigenous systems of medicine including Ayurveda, traditional Chinese medicine, and Unani are loosely based on the balance of such elemental substances or principles in the patient. Even as the practitioners emphasise their effectiveness and commonalities, mapping them to the framework of modern allopathic medicine has proven difficult. 

Let there be…nothing! 

Running along a roughly parallel track was the concept of a world made up of ‘the filled and the void’ - atomic corpuscles and empty space. From a philosophical point of view, this means that the atomists recognised non-being or nothingness to be as real as being or somethingness. About 400-500 BCE, Leucippus and his disciple Democritus devised the notion that there is an infinite number of hard, rigid, indivisible particles in constant and eternal motion, distinguished among themselves by their shape, arrangement, and position. Since they could be of any shape and were infinitely many, they could combine in an infinite number of ways to form the material world. The erstwhile primordial elements were ‘simply organisations of certain atoms’.² In the next century, their ideas were extended by Epicurus who thought that atoms in space do not just travel in straight lines under their own weight. If they did, they would simply ‘fall straight down through the depths of the void, like drops of rain, and no collision would occur, nor would any blow be produced among the atoms. In that case, nature would never have produced anything.’³ He went on to explain that these atoms deflect slightly from their paths every now and then in an unpredictable manner, causing them to run into each other and creating things. Approximately three centuries later, the Roman poet-philosopher Lucretius put Epicurus’ thoughts into the shape of a poem De Rerum Natura (On the Nature of Things) with his own poetic and philosophical flourishes. He named the unpredictable motion of atoms clinamen ⁴.  

Interestingly, Plato and Aristotle stood firmly in the anti-atomist camp. The Aristotelian view of science held sway in the western world throughout the middle ages and this has often been cited as the reason for the general stagnancy of the sciences during the period. Historians of science stand divided on this; however, intellectual exploration into such ideas remained mostly dormant in Europe until the Renaissance. 

In the Arab world of the 8^th to 12^th centuries CE, though, the debate on atomism was lively. Scholars like Ibn Sina wrote at length on the properties of jawhar, the Arabic equivalent of atoms, as eternal and unchangeable entities that combine to form the material world, while the likes of Al-Ghazali offered critiques and alternatives to the atomistic concept.

Atomism was a particularly vibrant theme in the intellectual life of the Indian subcontinent for thousands of years, reputedly pre-dating even the Greeks. The most mentioned name in this regard is that of Kanāda – a philosopher who lived in present-day India in the 6^th century BCE – who proposed the concept of anu as indivisible particles that form the basis of all matter, categorised based on qualities into five types, namely, earth, water, air, fire and space. Others in the same region had different and equally nuanced views on the matter which were mostly based on their religious leanings. 

Cogito, ergo ….um….?

These ancient concepts about the nature of matter can hardly be considered theories in the modern sense as they are not backed by experiments. Rather, they are philosophical propositions that are the products of thought. In most cases, they are also tangled with theology and metaphysics. They may seem to concur at several points with our own primary school conception of atoms, making it tempting to think that modern atomic theories are their direct heirs. Alan Chalmers⁵ is quick to point out that ‘the methods of experimental science are quite distinct from the methods involved in the development of philosophical matter theories’ and that it is a mistake to think that one foreshadowed the other. 

From the late 1500s to the early 1700s, the Renaissance in Europe sparked a revival of interest in science. Popularly known as the Scientific Revolution, this period saw experimental science gaining prominence and differentiating itself from philosophical theories about matter. Robert Boyle and Isaac Newton both built on the Greek legacy and were avid experimentalists but it would be a stretch to say that they verified their concepts about the structure of matter experimentally. According to Chalmers, the scientific revolution was truly revolutionary in that experimental science could progress without being excessively concerned about the true nature of matter itself. 

Yup, we can show it in the lab 

The progression of modern atomic theory is familiar to us. John Dalton's atomic theory proposed in the early 19th century laid the foundation by postulating that each element is composed of identical indivisible particles with specific properties, which combine in simple ratios to form compounds. While this sounds very much like the ideas of the atomists of old, there were two crucial differences: one, his experiments bore out the law of proportion that his model predicted; two, the properties of each atom were not prescribed by the model but were left to experimental determination. 

The discovery of subatomic particles such as electrons by J.J. Thomson in the late 19th century was followed by Thomson's plum pudding model where electrons were embedded in a positively charged sphere. Meanwhile, Gustav Kirchhoff had some colourful stories to tell about electromagnetic radiation which eventually led to his laws of spectroscopy where he explained the interaction between matter and light. Some of this work was extended upon by Max Planck around 1900. Many popular accounts^6,7 claim that it was Max Planck’s work on lightbulbs that led him to deduce that light energy (more specifically, black body radiation) is not emitted or absorbed in a continuous spectrum, but as discrete packets or ‘quanta’. However, there isn’t much in established works^8,9 of science history to lend credence to the lightbulb story. Be that as it may, it is interesting to note that initially for Planck, quanta were a mathematical shortcut than a reflection of reality – a neat little trick that would reconcile the formula with observation. It was Albert Einstein who, in 1905, used Planck’s ideas to explain the particle behaviour of light via the photoelectric effect and correlate the maths with the physical. The early 20^th century also saw Hans Geiger and Ernest Marsden, supervised by Ernest Rutherford, shoot alpha particles at a thin gold foil to find the nucleus. Even though Einstein’s work contributed to the understanding of wave-particle duality, it was Louis de Broglie that first postulated the dual nature of matter (1924) in no less than his PhD thesis. He won the Nobel Prize just five years later.

Talking it out like gentlemen…oh wait…there’s Marie Curie! 

The first Solvay Conference, an invitation-only event that discussed important unsolved problems in physics, was held in 1911. From the first conference in 1911 to the sixth in 1930, Marie Curie was the only woman to be invited. In 1933, Irene Joliot Curie and Lise Meitner were added to the guest list. According to Lambert,¹⁰ the 1911 conference is as legitimate a starting point for modern physics as Planck’s recognition of energy quanta in 1900 or the numerous new discoveries of the period including radio waves, the electron, radioactivity, and X-rays. This conference, he claims, indicated expert acknowledgement of the end of the classical era. 

The Rutherford-Bohr atom model is considered a direct outcome of the Solvay conference.¹⁰ In 1913, Neils Bohr introduced quantised electron orbits around the nucleus and explained atomic spectra and electron energy levels, thus revolutionising our understanding of atomic structure. 

Then came Heisenberg, Schrödinger and his cat, and Born, who brought to the fore the electrons' probabilistic behaviour in orbitals rather than fixed paths. This wave-particle duality concept, exemplified by Schrödinger's equation, led to quantum numbers that define electron properties more accurately. The equation describes the behaviour of quantum systems, including electrons in atoms. The electron cloud model replaced Bohr's orbits, with probable electron locations around the nucleus based on these quantum principles. Quantum field theory and the Standard Model expanded this understanding, defining particles and forces at a fundamental level. Thus, post-Bohr, atomic models shifted to probabilistic quantum descriptions, revolutionising our perception of the subatomic.

Is this thing a thing at all?!

Hereabouts, the world of science was at a juncture where ideas on atoms seemed to regress from the concrete and visual to the speculative and abstract. It is not easy to think of a thing that is at once a thing and a movement. Despite being upheld in all kinds of experiments, relating the mathematical theory of quantum mechanics to experienced reality requires much dexterous thought. The orthodox interpretation in textbooks is the Copenhagen Interpretation based on the views of Bohr and Heisenberg. This was challenged or modified to varying degrees of effectiveness by the pilot-wave interpretation, many-worlds interpretation, quantum informational approaches, relational quantum mechanics, QBism, consistent histories, ensemble interpretation, De Broglie-Bohm theory, transactional interpretation, Von Neumann-Wigner interpretation and even fringe ones like quantum mysticism. The philosophical implications of quantum mechanics were massive. According to some¹¹, it turns the tables on the materialism that the ancient atomists put forward. Others¹² differed in their opinions of what the different terms mean, the scope and nature of their applications and even how much of it is 'real'. 

Could you please write that down for me? 

Considering how complicated this whole quantum mechanics affair can be, it stands to reason that interested parties may need more than one set of tools to work with it. These take the form of groups of equations and principles and are known as formalisms. The choice of a formalism depends on the task at hand. There are three widely-used formalisms, namely the Schrödinger Picture or wave function formalism, the Heisenberg Picture or matrix mechanics and the Dirac Picture or Hilbert space formalism. The wave function formalism describes the quantum state of a system using wave functions and is particularly useful for understanding time evolution and predicting measurements. Matrix mechanics, on the other hand, centres around representing quantum states and operators as matrices, making it suitable for complex systems and calculations involving multiple particles. Dirac notation provides a concise and elegant way to express quantum states, operators and measurements, and is widely used in quantum information and computing. In fact, they represent the same ideas or describe the same physical reality in three mathematical languages and can be translated from one to another without loss of meaning. No one formalism is more correct than the other, leaving scientists free to choose whichever is suited to their purpose. 

The Schrödinger equation

Without much ado:

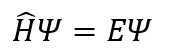
This little equation arguably carries all that one needs to know about a wave. Quantum mechanics presupposes the existence of a wavefunction

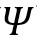
for each quantum system. A wavefunction under mathematical duress by different operators give us the details of the observables of the system such as position, momentum, spin and angular momentum. Broadly, an operator consists of a series of mathematical operations (including differentiation, matrix operations and vector algebra) that are applied to a wavefunction in a prescribed manner.  In the Schrödinger equation, the Hamiltonian

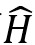
operator operates on

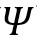
to give the energy E of the system. 

The wavefunctions for a few cases such as the free particle, harmonic oscillator, hydrogen atom and particle in a box can be wrestled out in an undergraduate course but these alone do not provide much insight into the system. A tiny upgrade of hydrogen to helium complicates matters so much that a complete analytic solution has never been found and much of science deals with systems more complex than a prodigal particle. How inconvenient!

Atom smushing for dummies

Theories are the stuff that science is made of. The American Association for the Advancement of Science defines a theory as ‘a well-substantiated explanation of some aspect of the natural world, based on a body of facts that have been repeatedly confirmed through observation and experiment.’ It explains how or why things are the way they are. A law of science is a statement of how facts relate to each other based on repeated experiments or observations. A theory is general while a law is applicable only in a particular range of conditions. A law answers no existential questions and offers no explanations, but simply sighs and says, ‘it is what it is’. 

It is tempting to think of science as the disinterested pursuit of explanations, but it does have to do work to pay the bills. So, enter the Model. 

A model is not always the assemblage of ping-pong balls and sticks that represent atoms and atomic bonds. Applying abstractions help scientists simplify a real system to an approximate representation (or model) that can then be used to understand the real system better.  It can be an abstract mathematical entity like the simple harmonic oscillator which is an imaginary object that obeys the force law F = -kx;  an imagined concrete thing like the periodic table in which each box corresponds to an actual element; an intermediary like a computer simulation that helps you examine a real system, or several other things depending on why and where they are deployed.¹³ John von Neumann had the right idea about what a model should do – ‘it is expected to work’.¹⁴

The foregoing section on quantum mechanics shows that some hacks might help make it more practical. If only those intractable equations could be smushed down into a manageable shape, quantum physicists could use the framework to tackle more complicated systems. Astronomers have modelled celestial motion and gotten away with it. The answers might not be exact but surely, could they not be good enough to work? 

What simplifying assumptions could they use to lure out a few observables from the quantum jungle? 

The heavyweights

For a hydrogen atom, the nucleus is 1,836 times heavier than an electron whizzing around it; for helium, this ratio is 7,358 and for uranium, it is a staggering 4,340,000. Hence, it is safe to assume that the heavy nuclei are stationary at the timescale of electronic motion. It follows then that the wavefunctions of the nuclei and the electrons can be considered separately, and for each (stationary) position of the nucleus, we only need to solve as many easy-to-solve one-electron Schrödinger’s equations as there are electrons in the system. This is the Born-Oppenheimer approximation. 

The Hamiltonian operator of a system represents the total energy of that system. For a typical atom, this includes the kinetic energy of the nucleus and the electrons, and potential energies due to electron-nucleus interaction, electron-electron repulsion, nucleus-nucleus repulsion, spin-orbit interaction, external potentials and relativistic corrections. The Born-Oppenheimer approximation splits this alphabet soup into the nuclear and electronic Hamiltonians and then effectively does away with the nuclear bit. 

Several roads that led to Rome

Around the same time (mid to late 1920s), Ralph Fowler at Cambridge University was shepherding a group of graduate students that included a certain Mr. Douglas Hartree and a Mr. Hilleth Thomas.¹⁵ Fowler had been the doctoral advisor to at least 64 students in his career including Paul Dirac, Lennard-Jones, S. Chandrasekhar, Nevill Mott and E A Guggenheim.¹⁶  

Thomas had, at the age of 10, read about the Bohr model. Despite Fowler being away in Copenhagen during the first year of Thomas’ PhD, he worked on ‘an old quantum mechanics problem’ and got both his first published paper and an award for it. Eventually, he set out on a different road from Schrödinger’s to describe electrons. He sought to look at the electrons statistically, considering not individual particles, but a smushed-up electron cloud having a uniform average electron density. Enrico Fermi had taken the same track independently. They formulated the kinetic energy based on a non-interacting, homogenous electron gas, providing a means to express the kinetic energy of an electron density function which is in turn a function of position. A function of a function is counterintuitively called a functional and thus, the Thomas-Fermi model represented a sort of prototypical Density Functional Theory (DFT).  As with every other model, it had limitations. Their representation of the kinetic energy was unacceptably simple and was not applicable to anything other than the simplest systems. Also, the classical Coulomb equation they chose to represent electron-electron repulsion did not consider the exchange and correlation energies that reflect the influence of electron spin states and other interactions. 

Hartree was a number-cruncher with a formidable reputation. During World War I, the 20-year-old devised efficient numerical methods to solve the analytically unsolvable differential equations for the motion of artillery shells under the action of drag and wind effects.¹⁷ He was interested in analysing the Bohr model with a quantitative eye and eventually set about proposing an approximate method to solve Schrödinger’s equation. His idea was to treat each electron in a many-electron system as a lonely particle that moves through an average-potential world. This average potential is created by the combined action of the nucleus and all the other electrons in the system, while electron-electron interactions were ignored. Thus, the unsolvable N-electron wavefunction could now be split into N solvable one-electron wavefunctions, provided the effect of the average field was factored in. He proposed the Hartree product which, in simple terms, says that an approximate solution of the N-electron wavefunction could be obtained from the product of all the one-electron wavefunctions that factor in it.  Hartree proposed starting the calculations with an approximate field like the Thomas-Fermi approximation, using the solution of the first step as the input for the second and so on until the input and output fields for all electrons become the same. While practical, the spin and correlation effects were neglected. 

This was later remedied by Vladimir Fock whose 1930 paper¹⁸ introduced the concept of using Slater determinants to construct a many-electron wave function that obeyed the Pauli exclusion principle, thus bringing in an ‘exchange term’.  

Thus were born the famed Thomas-Fermi Model and the Hartree-Fock Self-Consistent Field Method. Then a physicist came along a few years later to build on them and ended up walking away with one-half of a chemistry Nobel Prize.

A child of the war

The effect of war on the scientific enterprise is undeniable. Research priorities and funding are considerably influenced by military needs and many wartime technologies have made their way into daily life. War also shapes individual destinies. Walter Kohn was very much a child of the war. Had history kept the Jewish lad in Vienna where he was born, he might have become a printer of art postcards. Instead, the Nazi horror took the boy to a farm in Kent, an internment camp in Liverpool, aboard a captured Polish cruise ship-turned-troop transport across the Atlantic, to a series of war camps in Canada where the refugees organised themselves to gain an excellent if piecemeal education, and finally, to the University of Toronto, all before he turned eighteen.¹⁹

Just like a unicorn

In 1964, Kohn worked with Pierre Hohenberg to develop the Hohenberg-Kohn theorem which indicated that the ground-state wave function of a many-electron system can be found using the ground-state electron density. The theorem states that there exists a universal functional of the electron density which uniquely determines the total energy of the system for a given electron density. Moreover, among all possible electron densities, the true ground-state electron density is the one that minimises this universal functional. Exciting! 

Except, nobody knew how to find this universal functional. Just like a unicorn. 

Introverted electrons

The path to particle smushing is strewn with mathematical entities that hold the secrets of the universe if only someone could find them. The Hohenberg-Kohn theorem was a conceptual shoutout to the Thomas-Fermi model. How now, could the universal functional be tackled? By his own admission,²⁰ Kohn’s thoughts harked back to the Hartree-Fock equations, and in the summer of 1964, he had a postdoc – Lu Sham – with whom he set about “the task of extracting the Hartree equations from the Hohenberg-Kohn variational principle for the energy”. Just like Hartree expressed the many-electron Schrödinger equation as a set of one-electron Schrödinger equations, Kohn and Sham managed to express the electron density of the many interacting electrons using the electron densities of a set of fictitious electrons moving in an effective external potential. These fictitious electrons were quite an introverted bunch – they had no interaction with the other electrons – but taken together, they had the same electron density as the system that was being modelled. These are the famous Kohn-Sham equations. 

The total energy of this new system had three components – the energy associated with the fictitious stand-in electrons (computable), the energy associated with the effective external potential (computable), and the catch-all exchange-correlation energy for all the bits and bobs that had nowhere else to go (not directly computable). The exchange-correlation energy is quite small compared to the total energy but is especially important in systems with significant electron correlations, impacting properties like conductivity, optical behaviour, and chemical reactivity. Now, only this tiny piece of the energy puzzle is missing, and it is small enough to weather an approximation. Kohn and Sham assumed that the exchange-correlation energy density at any point in space depends only on the local electron density at that point. They called this the Local Density Approximation (LDA).  Once an approximation was chosen, the system of equations could be solved self-consistently to find an approximate solution for the many-electron system. Modern density functional theory was finally here, although it was a few decades before the scientific community recognised that it should stay and flourish.

And when they realised how awesome it was, the physicist Walter Kohn walked away with one-half of the chemistry Nobel Prize in 1998.

Getting things wrong the right way

It is a given that approximations are wrong in the absolute sense. However, the key to making them work is to get them wrong in the right way and to know exactly how wrong you are.  LDA was a great starting point for approximating the exchange-correlation energy. It worked well for calculating the bulk properties of solids especially away from finicky places like interfaces and surfaces where it was safe to assume that the electron density varied smoothly. When the density did vary locally, factoring in the rate of variation improved the approximation. Functionals of this form are called Generalised Gradient Approximations (GGAs), and some of the most popular GGAs are Perdew-Burke-Ernzerhof (PBE), Revised Perdew-Burke-Ernzerhof (RPBE), Perdew-Wang 91 (PW91), Becke88 Exchange and Perdew86 Correlation (B88-P86), and Tao-Perdew-Staroverov-Scuseria (TPSS). GGAs are well-suited for modeling molecular systems, including geometries, electronic structures, and spectroscopic properties, as well as for studying solid-state materials such as crystals, semiconductors and interfaces, providing accurate descriptions of electronic properties and reaction energetics in diverse systems. Later, hybrid functionals were developed that combined the advantages of both local and semi-local functionals with a fraction of the exact exchange. This approach improves the description of electronic correlation effects, making them suitable for predicting band gaps, reaction energetics and molecular geometries. Some of the most popular hybrid DFT functionals are B3LYP, PBE0, HSE06, BH&HLYP and M06-2X. 

Several hundred functionals have since been developed and many more will be. The choice of a functional can be straightforward or torture depending upon the task and a source of immense satisfaction or frustration depending on how far the deadline is.  

‍The electron smushing black box 

Somewhere in the recesses of our research group’s shared resource drives sits the magic folder that can significantly delay the chances of your degree if you pull the wrong thing out. That, dear friends, is the folder with the pseudopotentials. Pseudopotentials are used to represent the electron-nucleus interaction. When there are too many electrons about, modelling the full interaction accurately would require too much computing power. Many studies can get by with accurate valence electron calculations and smush the effect of the core electrons into an imaginary pseudopotential. It modifies the effective potential experienced by the valence electrons, effectively "removing" the core electrons from the computational domain while still accounting for their influence on valence electron behaviour. Popular variants include norm-conserving pseudopotentials, ultra-soft pseudopotentials, and projector-augmented wave (PAW) pseudopotentials. Choosing pseudopotentials involves considering factors such as accuracy, transferability across systems, computational efficiency, coverage of core and valence states, compatibility with the software in use and a fair bit of intuition.  

‍Quo vadis? 

In the initial days, DFT applications were predominantly related to thermochemistry. Molecular mechanics and semi-empirical quantum chemistry were the preferred choices for larger molecules. Despite advancements, the materials of interest then—like transition-metal catalysts and energy-related materials—remain relevant, although new classes like metal–organic frameworks have emerged. DFT is also being increasingly used for applications in biology and pharmacy. Better computing power, algorithms and machine learning promise user-friendly and adaptable methods for material characterisation. High-throughput materials design has profited immensely from DFT.  Scale-up efforts, though, should ideally be tempered with healthy skepticism and correlation with theory and experiment.²¹

Better functionals and more intuitive pseudopotentials are on the wish list for the majority, the “holy grails” can vary with discipline – the ability to handle protein molecules, better parallelisation, accurate representation of graphene behaviour^{22, 23} and so on.

From where we stand now, it is safe to assume that the future will see computers smush atoms in better ways.

Bridging mind and matter

In the beginning, the atom was conceived in the human mind; experimentation made it tangible reality, mind to matter; computational modelling seems to complete the cycle. At its core, DFT embodies a reductionist approach that aligns with the philosophical notion that complex phenomena can be understood through fundamental principles and underlying entities. However, DFT also grapples with the challenge of approximations. This tension between simplification and accuracy raises philosophical questions about the nature of scientific modelling, the trade-offs between simplicity and realism and the quest for a more comprehensive understanding of quantum behaviour. In a philosophical sense, DFT may even be considered a representation of the dialectical relation between mind and matter. 

Is it a wave or a particle?

Is it a real thing or a line of code?

Is it mind or matter?

Falling walls

What effect does computational chemistry have on society? As quaint as that sounds it is a question worth asking. The pursuit of knowledge costs money; being a chemist requires access to a lab – neither of which is available in plenty for many, not to mention the cultural and social aspects that affect the representation of women and minorities in science. The increasing acceptance of computational studies in basic science research may have helped many overcome these boundaries of access and resource-disparity and make their way into the research ecosystem. Computational chemistry ensured that chemistry can be done without glassware or fume hoods. It can be done while sheltering from a pandemic, caring for whānau, being in a remote location or weathering out political violence. 

And it is still good chemistry. 

Dedication

This article is an overtly triumphalist history. I realise that for each name that stood the test of time, there are hundreds who contributed but were reduced to a footnote, a number in a headcount, or more often to nothingness – women, migrants, indigenous people, members of the working class, people of colour, marginalised communities, people sidelined for their beliefs and those affected by the many forms of systemic discrimination. I dedicate these words to them whose names we do not know. 

References

1. Chattopadhyaya, D. Science and Society in Ancient India, Research India Publications: Calcutta, 1977.
2. Pullman, B. The Atom in the History of Human Thought, Oxford University Press: New York, 1998
3. Epicurus & Gerson, L. P. The Epicurus Reader: Selected Writings and Testimonia, Hackett Publishing Company: Indianapolis, 1994.
4. Greenblatt, S. The Swerve: How the World Became Modern, W. W. Norton & Company: New York, 2011.
5. Chalmers, A. The Scientist’s Atom and the Philosopher’s Stone, Springer Netherlands: Dordrecht, 2009.
6. Smith, T. P. How Big is Big and How Small is Small: The Sizes of Everything and Why, Oxford University Press: Oxford, 2013.
7. Stewart, I. In Pursuit of the Unknown: 17 Equations That Changed the World, Basic Books: New York, 20121
8. Kragh, H. Niels Bohr and the Quantum Atom: The Bohr Model of Atomic Structure 1913–1925, Oxford University Press: Oxford, 2012
9. Kuhn, T. S. Black-Body Theory and the Quantum Discontinuity, 1894–1912, University of Chicago Press: Chicago, 1987
10. Lambert, F.J. The European Physical Journal Special Topics 2015, 224, 2023-2040
11. Timpson, C.G. In Philosophy of Quantum Information and Entanglement; Bokulich, A., Jaeger, G., Eds.; Cambridge University Press: Cambridge, UK, 2010; pp. 208–228.
12. Schlosshauer, M.; Kofler, J.; Zeilinger, A. Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics 2013, 44, 222–230
13. Dupre, G. Review of Models and Modeling in the Sciences: A Philosophical Introduction, by Stephen M. Downes, Routledge: New York and London, 2020.
14. Von Neumann, J.; Brody, F.; Vamos, T., Eds. The Neumann Compendium, World Scientific: Singapore, 1995
15. Zangwill, A. Archive for History of Exact Sciences 2013, 67, 331-348
16. McCrea, W.H. Biographical Memoirs of Fellows of the Royal Society 2024.
17. Hartree, D.R. Biographical Memoirs of Fellows of the Royal Society 2024.
18. Fock, V. Zeitschrift für Physik A Hadrons and Nuclei 1930, 61, 126–148.
19. Zangwill, A. Archive for History of Exact Sciences 2014, 68, 775–848.
20. Kohn, W. Reviews of Modern Physics 1999, 71, 1253–1266.
21. Kulik, H.J. Israel Journal of Chemistry 2022, 62, e202100016.
22. Houk, K.N.; Liu, F. Accounts of Chemical Research 2017, 50, 539–543.
23. Olatomiwa, A.L. et al Heliyon 2023, 9, e14279

Biographical Information

Lekshmi Dinachandran is a PhD candidate at the University of Otago. She is a member of the Garden Group that specialises in computational chemistry. Her areas of interest include density functional theory, hydrogen storage and the history and philosophy of science.